Laboratoř technické matematiky

Oddělení:   Oddělení D 4 – Rázy a vlny v tělesech
 Vedoucí:   Ing. Martin Isoz, Ph.D.

Laboratoř technické matematiky (techMathGroup) se zabývá vývojem numerických metod a výpočetních algoritmů pro nelineární statické a dynamické problémy, které jsou součástí různých oblastí výpočetní mechaniky kontinua. Zajímáme se o systémy tekutina-částice s důrazem na nepravidelné částice a vyšetřování kontaktů v takových systémech. Kromě toho je značná pozornost věnována vývoji numerických nástrojů pro simulaci reaktivního heterogenně katalyzovaného nestlačitelného a neizotermického proudění a pro průmyslově využitelné simulace laserového vyklepávání. V neposlední řadě se zabýváme také redukcí řádu modelu, topologickou optimalizací a analýzou proudění.
laborator_technicke_matematiky_logo

Vývoj CFD-DEM řešiče a simulace turbulentního proudění s metodou vnořené hranice

OpenHFDIB-DEM je rozšířením knihovny OpenFOAM umožňujícím provádět simulace proudění s částicemi libovolného tvaru. Zahrnutí pevné fáze do CFD sítě je založeno na metodě vnořené hranice a implementové pomocí nástrojů dostupných v OpenFOAM. DEM část kódu je kompletně vyvíjená v Laboratoři technické matematiky, ale je kompatibilní s knihovnou OpenFOAM a celé softwarové řešení je monolitické, tzn. CFD má přístup ke všem proměnným používaným DEM a naopak. Kód je open-source a veřejně dostupný na githubu.

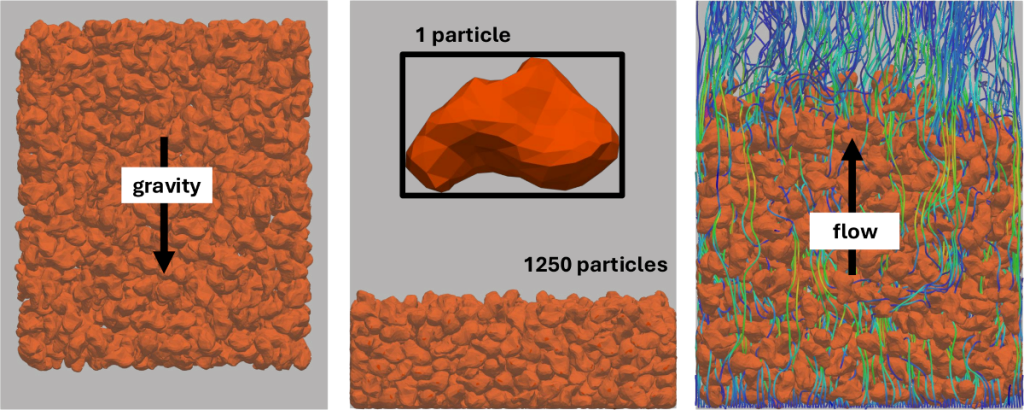
techMathGroup_OpenHFDIB-DEM_promo_image

Github repozitář: techMathGroup/openHFDIB-DEM

S výzkumem CFD-DEM souvisí i zkoumání možností propojení metod Reynoldsova středování pro simulaci turbulentního proudění s metodou vnořené hranice. Zde je cílem alespoň kvalitativně správně simulovat chování turbulentního proudění v blízkosti nerozlišeného vnořeného rozhraní kapalina-pevná látka. Jinými slovy, zabýváme se spojením metody vnořené hranice a stěnových funkcí. Kód je opět open-source a veřejně dostupný.

Github repozitář: techMathGroup/openHFDIBRANS

Výzkumný tým: M. Isoz, O. Studeník, L. Kubíčková, M. Dejaková, J. Terpáková

Spolupráce: Monolith Research Group, University of Chemistry and Technology, Czechia; School of Hydro Science & Engineering, Taiyuan University of Technology, China; Faculty of Natural Sciences, University Ústí nad Labem, Czechia; RED CFD Ltd., Italy; Exeter Small-Scale Robotics Laboratory, University of Exeter, United Kingdom

Související publikace:

[1] Isoz, M.; Kotouč Šourek, M.; Studeník, O.; Kočí, P.: Hybrid fictitious domain-immersed boundary solver coupled with discrete element method for simulations of flows laden with arbitrarily-shaped particles. Computers & Fluids, 244 (2022) 105538, DOI: 10.1016/j.compfluid.2022.105538
[2] Kotouč Šourek, M.; Studeník, O.; Isoz, M.; Kočí, P.: Viscosity prediction for dense suspensions of non-spherical particles based on CFD-DEM simulations. Powder Technology, 444 (2024) 120067, DOI: 10.1016/j.powtec.2024.120067

Simulace heterogenně katalyzovaného reaktivního proudění

Významná část našeho výzkumu je zaměřena na vývoj CFD řešičů pro heterogenně katalyzované reaktivní proudění. Naše řešiče jsou schopné simulovat neizotermní systémy s vysokými koncentracemi reagujících složek (je uvažován transport hmoty řízený Stefanovou-Maxwellovou difuzí). Všechny CFD kódy jsou naimplementovány v knihovně OpenFOAM. Spolupracujeme s několika českými i mezinárodními laboratořemi a aplikujeme tyto řešiče na reálné problémy.

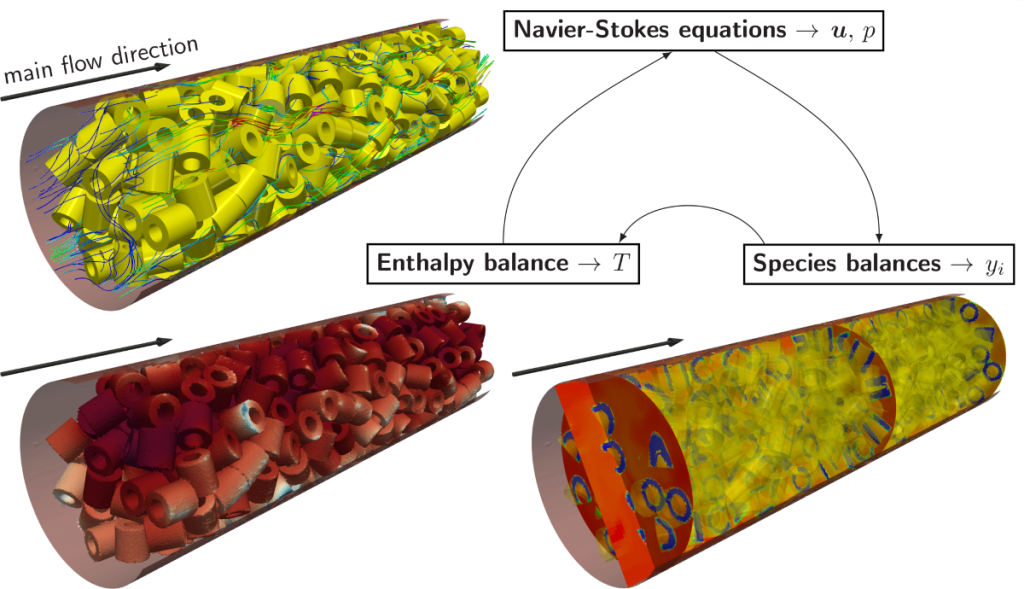
techMathGroup_reactFlow_promo

Výzkumný tým: T. Hlavatý, M. Isoz, M. Khýr, J. Rýc

Spolupráce: Monolith Research Group, University of Chemistry and Technology, Czechia; Department of Carbohydrates and Cereals, University of Chemistry and Technology, Czechia; Oak Ridge National Laboratory, United States of America; Faculty of Natural Sciences, University Ústí nad Labem, Czechia; BEAS, a.s., Czechia

Související publikace:

[1] Isoz, M; Haidl, J.: Computational-fluid-dynamics analysis of gas flow through corrugated-sheet-structured packing: Effects of packing geometry. Industrial & Engineering Chemistry Research, 57 (2018), 11785-11796, DOI: 10.1021/acs.iecr.8b00676
[2] Kočí, P.; Isoz, M.; Plachá, M.; Arvajová, A.; Václavík, M.; Svoboda, M.; Price, E.; Novák, V.; Thompsett, D;: 3D reconstruction and pore-scale modeling of coated catalytic filters for automotive exhaust gas aftertreatment. Catalysis Today, 320 (2019), 165-174, DOI: 10.1016/j.cattod.2017.12.025
[3] Wehinger, G.D.; Ambrosetti, M.; Cheula, R.; Ding, Z.-B.; Isoz, M.; Kreitz, B.; Kuhlmann, K.; Kutscherauer, M.; Niyogi, K.; Poissonnier, J.; Réocreux, R.; Rudolf, D.; Wagner, J.; Zimmermann, R.; Bracconi, M.; Freund, H.; Krewer, U.; Maestri, M.: Quo vadis multiscale modeling in reaction engineering? - A perspective. Chemical Engineering Research And Design, 184 (2022), 39-58, DOI: 10.1016/j.cherd.2022.05.030
[4] Hlavatý, T.; Kočí, P.; Isoz, M.; Deka, D.; Partridge, W.: Balanced Fast-SpaciMS capillary configurations provide practically noninvasive channel-average measurements in catalytic monoliths. Chemical Engineering Science, 282 (2023), 119272, DOI: 10.1016/j.ces.2023.119272

Konečně objemové simulace laserového vyklepávání

Nejvíce aplikovaným problémem řešeným v Laboratoři technické matematiky je vývoj metod pro průmyslové simulace laserového vyklepávání (LSP). Celý simulační rámec je implementován pomocí knihovny OpenFOAM, která je založena na metodě konečných objemů. V důsledku toho lze LSP, které zahrnuje šíření elastoplastické rázové vlny s časovým rozsahem v nanosekundách a amplitudou v GPa, simulovat i na nedokonalých sítích.

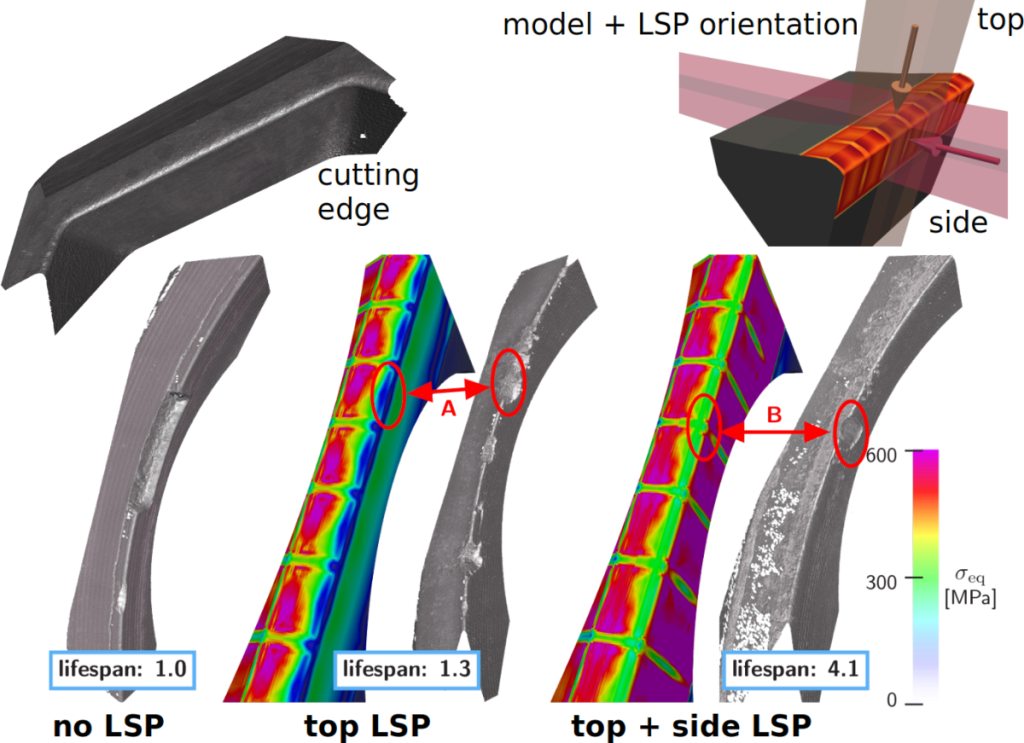
techMathGroup_LSP_promo

Výzkumný tým: M. Isoz, P. Gruber, D. Voborský

Spolupráce: HiLASE Centre, Institute of Physics of the Czech Academy of Sciences, Czechia; SHM, s.r.o., Czechia; Centrum Výzkumu Řež s.r.o., Czechia; COMTES, FHT a.s.; Embraer, Brazil; Welle Laser Technology, Brazil; EMBRAPII Unit Laser Technologies, Brazil

Optimalizace a redukce řádu modelu

Aby bylo možné aplikovat komplexní modely vyvíjené v rámci ostatních výzkumných zaměření naší laboratoře na reálné optimalizační úlohy využitelné v průmyslu, jsme aktivní ve dvou vzájemně provázaných odvětvích: (i) vývoj metod pro vícekriteriální topologickou a tvarovou optimalizaci i optimalizaci obecně, (ii) vývoj metod pro a-posteriori redukci řádu modelu, a to včetně projekčních metod a technik založených na využití umělé inteligence.

Významným výsledkem v této oblasti je vývoj algoritmu pro tvarovou optimalizaci s využitím CFD. Tento algoritmus vychází z evolučních algoritmů (NSGA-II), ale je obohacen o adaptivní výběr vzorků a trénování umělé inteligence jakožto náhradního modelu. Celkově je tento přístup schopen významně zrychlit pozdější stadia optimalizace a oproti čisté optimalizaci nalézt bohatší množinu pareto-optimálních řešení. Algoritmus je open source a volně přístupný veřejnosti.

techMathGroup_optim_promo

Github repozitář: techMathGroup/CFDNNetAdapt

Dále se věnujeme vývoji technik redukce řádu modelu pro systémy s dominantním transportem. Námi vyvíjená metoda se nazývá Vlastní ortogonální rozvoj s posuvem a s interpolací pomocí umělých neuronových sítí (angl. shifted proper orthogonal decomposition with interpolation via artificial neural networks, sPODIANN) a kombinuje techniky kompenzace transportu, které umožňují dobře aproximovat data strukturami s nízkou hodností, s umělými neuronovými sítěmi, které poskytují hledaný nízkodimenzionální model. Vývoj metody sPODIANN je motivován převážně snahou o umožnění výpočetně proveditelných parametrických studií systémů simulovaných pomocí CFD-DEM.

V neposlední řadě využíváme vlastní ortogonální rozvoj (proper orthogonal decomposition, POD), rozvoj do dynamických módů (dynamic mode decomposition, DMD), a metody založené na analýze obrazu, za účelem analyzování dynamického turbulentního proudění a validace jeho simulací.

Výzkumný tým: L. Kubíčková, A. Kovárnová, M. Isoz, M. Belda, T. Hlavatý, I. Havlenová

Spolupráce: I2M, Aix-Marseille Université, France; Institute for Hydrodynamics, Czech Academy of Sciences, Czechia

Související publikace:

[1] Isoz, M.: POD-DEIM based model order reduction for speed-up of flow parametric studies. Ocean Engineering, 186 (2019) 106083, DOI: 10.1016/j.oceaneng.2019.05.065

MKP systém PMD (Package for Machine Design)

PMD je moderní výpočetní soubor programů na základě metody konečných prvků (MKP), který je nezávislý na platformě. Systém je určen pro všeobecné inženýrské problémy v mechanice kontinua tuhých těles. Jde o proprietární kód s dlouhou, 35letou tradicí, který je v současnosti udržován a vyvíjen zaměstnanci Laboratoře výpočetní mechaniky těles. Další informace o systému PMD naleznete zde.

Řešitelé: J. Dobiáš, D. Gabriel, J. Kopačka, R. Marek, J. Masák, J. Novotný, P. Pařík, J. Plešek, S. Pták

Spolupráce: VAMET, s.r.o.

Výpočty v rámci výzkumu skupiny techMathGroup zajišťuje lokální HPC cluster v Ústavu termomechaniky AV ČR. Od roku 2024 se cluster skládá z 656 výpočetních jader uspořádaných do 15 uzlů. Celková dostupná paměť RAM je 4 160 TB. Nicméně, klastr je pravidelně aktualizován a zde uvedené informace nemusí být akutuální.

Skupina disponuje odbornými znalostmi zahrnujícími využívání několika balíčků a programovacích prostředí, z nichž všechny jsou open-source. Naše práce je postavena především na C++ CFD knihovně OpenFOAM, která je založena na metodě konečných objemů. Dále máme zkušenosti s programováním v jazycích python a bash a s používáním programů Blender a Paraview, zejména pro přípravu geometrií systémů a následné zpracování výsledků. Výzkum související s umělou inteligencí probíhá s využitím TensorFlow/Keras.

Ing. Ondřej Ježek

Ing. Tomáš Hlavatý

  • Téma: Matematické modelování a redukce řádu modelu v reaktivních prouděních
  • Školitel: prof. Jiří Furst, Ph.D.
  • Konzultant: Ing. Martin Isoz, Ph.D.
  • Počátek studia: 2022
  • Předpokládaný rok obhajoby: 2026

Ing. Ondřej Studeník

  • Téma: Vývoj CFD-DEM metod pro simuace pohybu a interakcí pevných částic v heterogenních reaktorech
  • Školitel: prof. Petr Kočí, Ph.D.
  • Konzultant: Ing. Martin Isoz, Ph.D.
  • Počátek studia: 2022
  • Předpokládaný rok obhajoby: 2026

Ing. Kristýna Idžakovičová

  • Téma: Výpočetně providitelný model flokulace v míchaných nádobách
  • Školitel: Ing. Jan Haidl, Ph.D.
  • Konzultants: Ing. Martin Isoz, Ph.D.; doc. RNDr. Martin Pivokonský, Ph.D.
  • Počátek studia: 2022
  • Předpokládaný rok obhajoby: 2026

Ing. Lucie Kubíčková

  • Téma: Topologická optimalizace v chemicko-inženýrských aplikacích
  • Školitel: Ing. Martin Isoz, Ph.D.
  • Konzultant: Ing. Jan Haidl, Ph.D.; prof. Ing. Miroslav Šóoš, Ph.D.
  • Počátek studia: 2023
  • Předpokládaný rok obhajoby: 2027

Ing. Marek Belda

  • Téma: Vývoj nových technik validace numerických modelů dynamického proudění
  • Školitel: doc. Ing. Tomáš Hyhlík, Ph.D.
  • Konzultant: Ing. Martin Isoz, Ph.D.
  • Počátek studia: 2023
  • Předpokládaný rok obhajoby: 2027

Ing. Anna Kovárnová

  • Téma: Redukce řádu modelu a optimalizace v inženýrských aplikacích
  • Školitel: Ing. Martin Isoz, Ph.D.
  • Konzultant: doc. Ing. Jan Švihlík, Ph.D.
  • Počátek studia: 2024
  • Předpokládaný rok obhajoby: 2028