Recent experiments identified significant torsional self-exciting forces, leading to the development of a new analytical model calibrated with NACA 0010 blade data. A critical advancement was the transition from a “planar contact” friction model to an “edge contact” model for torsional vibration, which more accurately accounts for relative rotation and crossing of contact surfaces.
Numerical simulations of the bladed wheel demonstrated that without damping, aeroelastic (AE) coupling leads to an exponential increase in amplitudes—a flutter state. However, by implementing dry-friction couplings in the tie-bosses and shrouds, the flutter was successfully suppressed, reducing vibration amplitudes by an order of magnitude and eliminating the dominance of the torsional resonant frequency in the spectrum.
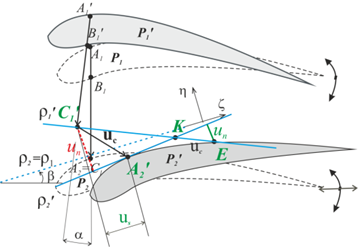
Figure 1b – Kinematics of edge contact models for neighboring profiles P1 and P2
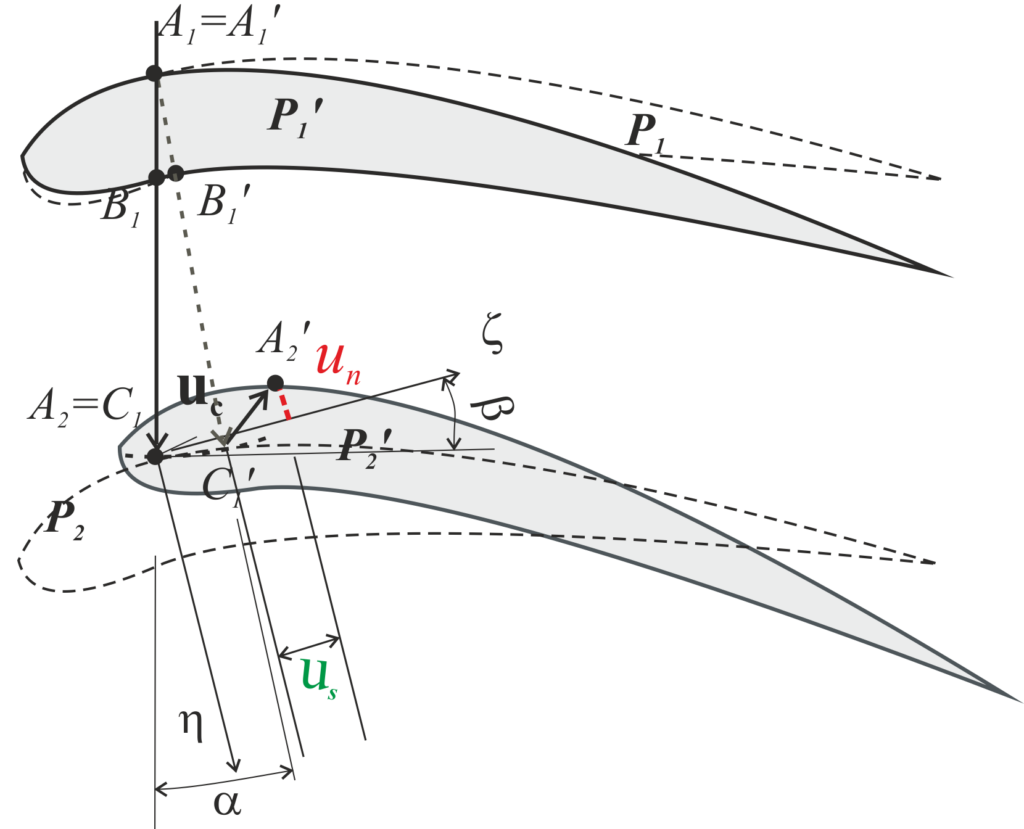
Figure 1a – Kinematics of planar contact models for neighboring profiles P1 and P2
General N-profile model accounting for interactions between adjacent blades was formulated (Fig. 2). A particular implementation of this model was implemented for a model that has 13 profiles (blades).
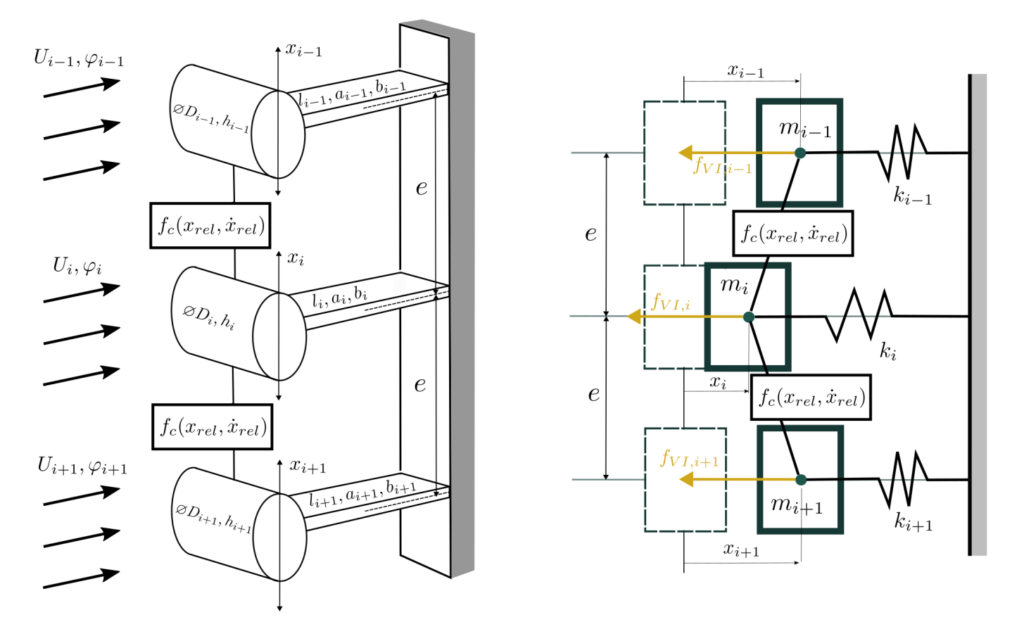
Figure 2 – Model of two vibrating and mutually interconnected profiles with the influence of mutual nonlinear interactions
Results gained using model with two profiles show that the presence of nonlinear coupling results in vibration synchronization and to the fact that because of the synchronization, the out-of-phase vibration mode during lock-in regime does not exhibit, Fig. 3.
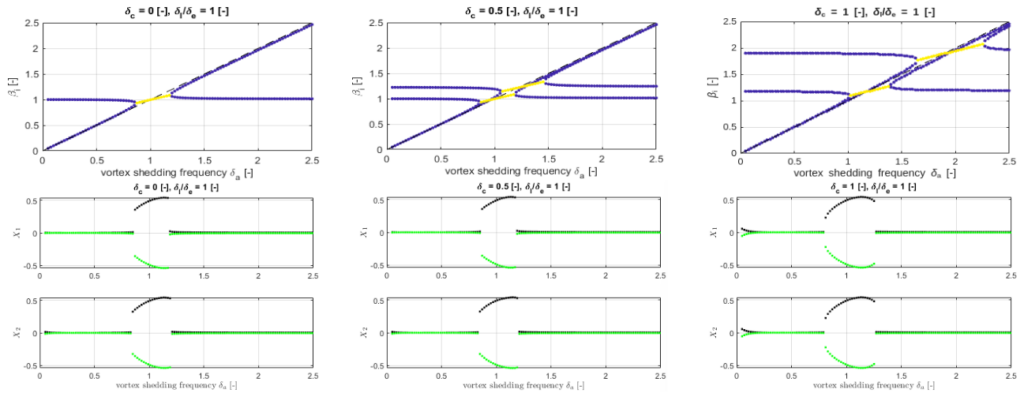
Figure 3 – Comparison of linearized models results (upper row) and amplitude characteristics from time simulation using nonlinear model, which leads to synchronization
